Course Description

Machine learning algorithms are data analysis methods which search data sets for patterns and characteristic structures. Typical tasks are the classification of data, automatic regression and unsupervised model fitting. Machine learning has emerged mainly from computer science and artificial intelligence, and draws on methods from a variety of related subjects including statistics, applied mathematics and more specialized fields, such as pattern recognition and neural computation. Applications are, for example, image and speech analysis, medical imaging, bioinformatics and exploratory data analysis in natural science and engineering:


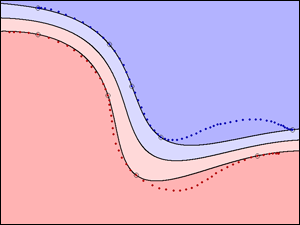
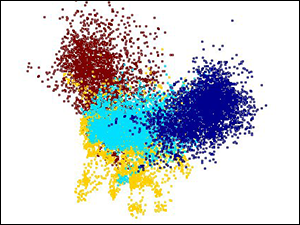
nonlinear decision boundary linear discriminant analysis gene expression levels
Non-linear decision boundary of a trained support vector machine (SVM) using a radial-basis function kernel. Fisher's linear discriminant analysis (LDA) of four different auditory scenes: speech, speech in noise, noise and music. Gene expression levels obtained from a micro-array experiment, used in gene function prediction.

We assume that students are familiar with the course Introduction to Machine Learning.

Announcements

Syllabus

Week Lecture topics Lecture slides References Tutorial slides Exercises
38 Introduction to AML Course Information
Lecture 1 		Bishop, Ch. 9 and 12 No tutorial No exercise
39 Representations, measurements, data types Notes
Lecture 2 		Bishop, Ch. 9 and 12 Exercise 1
Solution 1
40 Density estimation Lecture 3
Notes 		Wasserman, Ch. 9 -- 13, Slides No Exercise
41 Regression, bias-variance tradeoff Lecture 4 Hastie, Sec 3.2, 3.4, and 3.6 Slides Exercise 2
Solution 2
42 Gaussian Processes Lecture 5 Bishop, Sec 6.4
Model Selection for GP 		Exercise 3
Solution 3
43 Model validation (numerical techniques) Lecture 6 Bishop, Ch. 7
Boyd and Vanderberghe, Ch. 5 		Project 1 No exercise
44 SVMs Shockfish
Lecture 7 		Bishop, Ch. 7
Joachims, 2009 		Slides Exercise 4
Solution 4
45 Ensemble methods Lecture 9 Hastie, Sec 8.7, 10.1 -- 10.11
Wyner et al, 2018 		Recording Exercise 5
Solution 5
46 Deep learning Lecture 10
Lecture 10b
Random Forests as Classifiers 		Goodfellow, Sec. 6.5, 8.1, 8.3.1 Project 2
Notebook 		No exercise
47 Deep learning Lecture 11
Notes 		Goodfellow, Sec. 6.5, 8.1, 8.3.1
Exercise 6
Solutions 6
48 Deep learning Lecture 12
Notes 1
Notes 2
Notes 3 		Goodfellow, Sec. 6.5, 8.1, 8.3.1

 Slides Exercise 7
Solutions 7
49 Non-parametric Bayesian methods Lecture 13
Lecture 13b 		Murphy, Ch. 24, 25
Kamper's notes
Gershman and Blei's tutorial 		Slides No exercise
50 PAC learning Lecture 14
PAC Notes 		Mohri, Ch. 1 Exercise 8
Solutions 8
51 PAC learning Lecture 15
Notes 		Mohri, Ch. 1 Slides
Recording 		Exercise 9
Solutions 9

Some of the material can only be accessed with a valid nethz account. This list of topics is intended as a guide and may change during the semester.

General Information

Course Catalogue (VVZ)

Times and Places

Lectures
Time Room Remarks
Thu 15-16 ETA F 5
Fri 08-10 HG F 7 | HG F 5 (video)
Tutorials

Please attend only the tutorial assigned to you by the first letter of your surname.

Time Room Surname first letter
Wed 14-16 CAB G 61 A-L
Fri 14-16 CHN C 14 M-Z

All tutorial sessions are identical. Attendance to the tutorials is not mandatory.

Exercises

The exercise problems will contain theoretical pen & paper assignments. Solutions are not handed in and are not graded. Solutions to the exercise problems are published one week after the exercise on this website.

Projects

The goal of the practical projects is to get hands-on experience in machine learning tasks. For further information and to access the projects, login at the projects website using your nethz credentials. You need to be within the ETH network or connected via VPN to get access.

There will be one "dummy" project (Task 0) whose purpose it is to help students familiarize with the framework we use and which will be discussed in the tutorials of the third week of the semester. Following that, there will be three "real" projects (Task 1 -- Task 3) that will be graded.

In order to complete the course, students have to pass at least two out of the three graded projects (it is recommended to participate in all three). Students who do not fulfil this requirement will not be admitted to take the final examination of the course.

The final project grade, which will constitute 30% of the total grade for the course, will be the average of the best two project grades obtained.

Release dates and submission deadlines are in (UTC time)

Release date Submission deadline
Task 0 (dummy task) Mon, Oct 2, 15:00 Mon, Oct 23,14:00
Task 1 Mon, Oct 23, 15:00 Mon, Nov 13, 14:00
Task 2 Mon, Nov 13, 15:00 Mon, Dec 4, 14:00
Task 3 Mon, Dec 4, 15:00 Fri, Dec 23, 14:00

Exam

There will be a written exam of 180 minutes length. The language of the examination is English. As written aids, you can bring two A4 pages (i.e., one A4 sheet of paper), either handwritten or 11 point minimum font size. The grade obtained in the written exam will constitute 70% of the total grade.

Under certain circumstances, exchange students may ask the exams office for a distance examination. This must be organized by you via the exams office with plenty of time in advance. Prof. Buhmann does not organize distance exams.

Moodle

To account for the scale of this course, we will answer questions regarding lectures exercises and projects on Moodle. To allow for an optimal flow of information, please ask your content-related questions on this platform rather than via email. In this manner, your question and our answer are visible to everyone. Consequently, please read existing question-answer pairs before asking new questions.

Text Books

C. Bishop. Pattern Recognition and Machine Learning. Springer 2006.
This is an excellent introduction to machine learning that covers most topics which will be treated in the lecture. Contains lots of exercises, some with exemplary solutions. Available from ETH-HDB and ETH-INFK libraries.

R. Duda, P. Hart, and D. Stork. Pattern Classification. John Wiley & Sons, second edition, 2001.
The classic introduction to the field. An early edition is available online for students attending this class, the second edition is available from ETH-BIB and ETH-INFK libraries.

Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. Deep learning. MIT Press, 2016.

T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning: Data Mining, Inference and Prediction. Springer, 2001.
Another comprehensive text, written by three Stanford statisticians. Covers additive models and boosting in great detail. Available from ETH-BIB and ETH-INFK libraries. A free pdf version is available.

Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of machine learning. MIT press, 2018.

L. Wasserman. All of Statistics: A Concise Course in Statistical Inference. Springer, 2004.
This book is a compact treatment of statistics that facilitates a deeper understanding of machine learning methods. Available from ETH-BIB and ETH-INFK libraries.

D. Barber. Bayesian Reasoning and Machine Learning. Cambridge University Press, 2012.
This book is a compact and extensive treatment of most topics. Available for personal use online: Link.

K. Murphy. Machine Learning: A Probabilistic Perspective. MIT, 2012.
Unified probabilistic introduction to machine learning. Available from ETH-BIB and ETH-INFK libraries.

S. Shalev-Shwartz, and S. Ben-David. Understanding Machine Learning: From Theory to Algorithms. Cambridge University Press, 2014.
This recent book covers the mathematical foundations of machine learning. Available for personal use online: Link.

Exams from previous years

FAQ

Q: Can I transfer my project grades from last year to this year? No.

Q: Can I take the exam remotely? This is only possible for exchange students or rare exceptions. You must make a justified request to the exams office early in the semester. Prof. Buhmann does not handle such requests.

Q: When do we get the project grades? At the end of the course, but you are informed before the exam whether you passed enough projects.

Q: I cannot attend the tutorial I have been assigned to, can I attend another tutorial? Yes, but please wait until a few weeks for this. During the first weeks, we have a lot of students attending the tutorials, so we cannot accommodate all students in one room.

Q: I did not take introduction to machine learning at ETH. Can I still attend this course? How do I know if I have enough background for it? We cannot decide this for you. We recommend that you go through the material and the exam of introduction to machine learning. If you are familiar with the concepts taught there, you should probably be able to attend this course. You can also try to solve the exercise sheets for the first two weeks. If you can solve them, you are probably able to attend this course.

Q: I am a doctoral student and I want to get credits for this course. What do I need for this? You need to pass both the projects and the exam. We do not give partial credits for passing only the projects.

Q: Will a repetition of the final exam be offered in summer? Yes.

Contact

Please ask questions related to the course using Moodle, not via email.

Instructors: Prof. Joachim M. Buhmann, Teaching Assistants: João Carvalho (Head TA), Javier Abad, Sonali Andani, Florian Barkmann, Piersilvio Bartolomeis, Berken Demirel, Robin Geyer, Yongjun He, Fabian Laumer, Xia Li, Xiaozhong Lyu, Alexander Marx, Max Möbus, Stefan Stark, Alexandru Tifrea, Josephine Yates